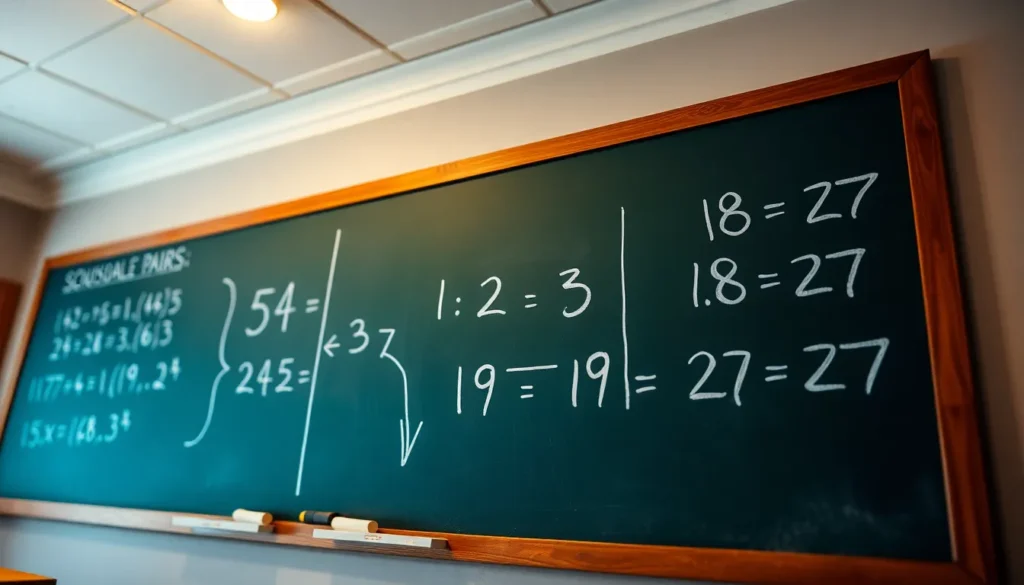When it comes to numbers, 54 isn’t just another face in the crowd; it’s a party waiting to happen. With its unique blend of factors, this number brings friends along for the ride, and those friends come in pairs. Understanding these pairs isn’t just a math exercise; it’s a gateway to unlocking the secrets of multiplication and division.
Table of Contents
ToggleUnderstanding Factors
Factors represent numbers that evenly divide into another number. The number 54 has several factors, and identifying them enhances understanding of its properties and relationships.
What Are Factors?
Factors refer to whole numbers that can be multiplied together to produce another number. For instance, factors of 54 include 1, 2, 3, 6, 9, 18, 27, and 54. Each factor pairs with another to yield 54 through multiplication. For example, 2 pairs with 27 since 2 multiplied by 27 equals 54. Recognizing these pairs provides insight into the structure of the number and reveals its divisibility traits.
Importance of Factors in Mathematics
Factors play a crucial role in various areas of mathematics. They simplify fractions, enable problem-solving in algebra, and contribute to a deeper understanding of multiplication and division concepts. In factoring polynomials, identifying factors allows for simplification and solving equations. Additionally, the concept of factors is fundamental in number theory, aiding in the exploration of prime numbers and their relationships. Understanding factors elevates mathematical comprehension and enhances overall numeracy.
Factors of 54
Factors reveal much about the number 54, showcasing how it divides evenly into whole numbers. The significance of these factors lies in their multiplication pairs, which contribute to understanding the structure and properties of 54.
Listing the Factors of 54
The factors of 54 include 1, 2, 3, 6, 9, 18, 27, and 54. Each of these numbers divides 54 evenly without leaving a remainder. For example, pairing 1 with 54 demonstrates the simplest relationship, while pairing 2 with 27 also yields the product 54. The factor pairs are:
- 1 and 54
- 2 and 27
- 3 and 18
- 6 and 9
Recognizing these pairs enhances insights into multiplication and divisibility.
Prime Factorization of 54
Prime factorization breaks down 54 into its most basic building blocks. The process reveals that 54 equals 2 times 3 squared. Specifically, it can be expressed as:
[
54 = 2 times 3^3
]
This factorization highlights the foundational nature of 2 and 3 in composing the number 54. Understanding this composition aids in various mathematical applications, such as simplifying fractional expressions and solving complex equations.
Factors of 54 in Pairs
Factors of 54 manifest in distinct pairs that multiply to give 54. Understanding these relationships aids in grasping the number’s composition and significance.
Identifying Factor Pairs
Identifying factor pairs involves recognizing which whole numbers divide evenly into 54. Each factor in a pair pairs with another to yield the total of 54. The pairs include (1, 54), (2, 27), (3, 18), and (6, 9). Each of these pairs showcases a unique relationship. Recognizing these pairs enhances comprehension of multiplication and division concepts.
Examples of Factor Pairs
Examples of factor pairs for the number 54 illustrate their unique properties. The pair (1, 54) reveals that 1 multiplied by 54 equals 54, emphasizing that any number multiplied by 1 itself remains the same. The pair (2, 27) shows that 2 multiplied by 27 also yields 54, indicating that 2 is a factor. Similarly, (3, 18) and (6, 9) demonstrate equal contributions towards building the total. Each of these pairs reinforces the importance of factors in number theory and practical applications in mathematics.
Applications of Factor Pairs
Factor pairs of the number 54 play a significant role in various real-world scenarios, helping to simplify complex calculations. For instance, businesses often use these pairs in inventory management to calculate optimal stock quantities efficiently. In construction, workers apply factor pairs to determine dimensions when creating structures, ensuring materials fit precisely. Education also benefits, as teachers use factor pairs to enhance students’ understanding of multiplication.
Real-World Applications
In practical contexts, factor pairs simplify everyday calculations. Farmers, for example, utilize them when determining crop yields from different plots of land. Retailers can analyze product combinations to maximize sales, using factors to explore pricing strategies. Event organizers apply these pairs during seating arrangements, ensuring guests fit in designated spaces without any waste. Each of these instances illustrates how well factor pairs contribute to problem-solving in daily life.
Importance in Problem Solving
Problem-solving benefits from understanding factor pairs, particularly in mathematics. When tackling equations, students find factor pairs useful for simplifying fractions and identifying common divisors. They help in breaking down complex algebraic expressions into manageable components. Furthermore, using factor pairs allows for quick calculations while analyzing patterns in numbers. This understanding strengthens students’ mathematical foundations, paving the way for more advanced studies.
The exploration of factor pairs of 54 reveals much more than simple arithmetic. Each pair serves as a building block for understanding the number’s structure and its divisibility properties. Recognizing these pairs not only enhances mathematical comprehension but also shows their practical applications in various fields.
From inventory management to educational settings, the significance of these factors extends into everyday life. By grasping the relationships between these pairs, individuals can simplify complex calculations and develop a stronger foundation in mathematics. Ultimately, the study of 54 and its factors enriches one’s appreciation for numbers and their interconnectedness.